Bài toán – Mạng tế bào (Dành cho học sinh THPT)
Mạng tế bào có dạng một lưới ô vuông hình chữ nhật. Tại mỗi nhịp thời gian: mỗi ô của lưới chứa tín hiệu là 0 hoặc 1 và có thể truyền tín hiệu trong nó cho một số ô kề cạnh theo một qui luật cho trước. Ô ở góc trên bên trái có thể nhận tín hiệu từ bên ngoài đưa vào. Sau nhịp thời gian đó, tín hiệu ở một ô sẽ là 0 nếu tất cả các tín hiệu truyền đến nó là 0, còn trong trường hợp ngược lại tín hiệu trong nó sẽ là 1. Một ô không nhận được tín hiệu nào từ các ô kề cạnh với nó sẽ giữ nguyên tín hiệu đang có trong nó. Riêng đối với ô trên trái, sau khi truyền tín hiệu chứa trong nó đi, nếu có tín hiệu vào thì ô trên trái sẽ chỉ nhận tín hiệu này, còn nếu không có tín hiệu nào thì ô trên trái cũng hoạt động giống như các ô khác. ở trạng thái đầu tín hiệu trong tất cả các ô là 0.
Yêu cầu: Cho trước số nhịp thời gian T và dãy tín hiệu vào S là một dãy gồm T ký hiệu S1, …, ST, trong đó Si là 0 hoặc 1 thể hiện có tín hiệu vào, ngược lại Si là X thể hiện không có tín hiệu vào tại nhịp thời gian thứ i (1<= i <= T), hãy xác định trạng thái của lưới sau nhịp thời gian thứ T.
Dữ liệu: vào từ file văn bản P3.INP:
– Dòng đầu tiên chứa 3 số nguyên M, N, T theo thứ tự là số dòng, số cột của lưới và số nhịp thời gian (1<M, N <= 200; T <= 100);
– Dòng thứ hai chứa xâu tín hiệu vào S;
– M dòng tiếp theo mô tả qui luật truyền tin. Dòng thứ i trong số M dòng này chứa N số ai1, ai2, …, aiN, trong đó giá trị của aij sẽ là 1, 2, 3, 4, 5, 6, 7, 8 tương ứng lần lượt nếu ô (i, j) phải truyền tin cho ô kề cạnh bên trái, bên phải, bên trên, bên dưới, bên trên và bên dưới, bên trái và bên phải, bên trên và bên trái, bên dưới và bên phải (xem hình vẽ); còn nếu ô (i, j) không phải truyền tín hiệu thì aij = 0.

Kết quả: Ghi ra file văn bản P3.OUT gồm M dòng, mỗi dòng là một xâu gồm N ký tự 0 hoặc 1 mô tả trạng thái của lưới sau nhịp thời gian thứ T.
Ví dụ:
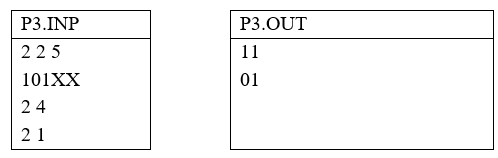
Quá trình biến đổi trạng thái được diễn tả trong hình dưới đây:

Giải bài toán – Mạng tế bào
Để giải bài toán này, chúng ta có thể sử dụng một thuật toán đệ quy để tính trạng thái của lưới sau mỗi nhịp thời gian T.
Dưới đây là mã giả của thuật toán:
Input: M, N, T, S, A (dữ liệu đầu vào)
Output: grid (trạng thái của lưới sau nhịp thời gian T)
1. Đọc dữ liệu đầu vào M, N, T, S, A
2. Khởi tạo một ma trận grid[M][N] với giá trị ban đầu là 0
3. Đặt trạng thái ban đầu của lưới grid[0][0] là giá trị của S
4. Duyệt qua từng nhịp thời gian i từ 1 đến T:
– Duyệt qua từng ô của lưới từ trên xuống dưới, từ trái sang phải:
– Nếu ô đó không nhận được tín hiệu từ các ô kề cạnh, giữ nguyên giá trị hiện tại của nó
– Ngược lại, tính giá trị mới của ô đó dựa trên qui luật truyền tin A[i-1][j] và trạng thái của các ô kề cạnh:
– Nếu A[i-1][j] = 1 (truyền tin cho ô bên trái), grid[i][j] = grid[i][j-1]– Nếu A[i-1][j] = 2 (truyền tin cho ô bên phải), grid[i][j] = grid[i][j+1]– Nếu A[i-1][j] = 3 (truyền tin cho ô bên trên), grid[i][j] = grid[i-1][j]– Nếu A[i-1][j] = 4 (truyền tin cho ô bên dưới), grid[i][j] = grid[i+1][j]– Nếu A[i-1][j] = 5 (truyền tin cho cả ô bên trên và bên dưới), grid[i][j] = grid[i-1][j] OR grid[i+1][j]– Nếu A[i-1][j] = 6 (truyền tin cho cả ô bên trái và bên phải), grid[i][j] = grid[i][j-1] OR grid[i][j+1]– Nếu A[i-1][j] = 7 (truyền tin cho cả ô bên trên và bên trái), grid[i][j] = grid[i-1][j] OR grid[i][j-1]– Nếu A[i-1][j] = 8 (truyền tin cho cả ô bên dưới và bên phải), grid[i][j] = grid[i+1][j] OR grid[i][j+1]5. Ghi kết quả vào file P3.OUT theo định dạng yêu cầu.
Cài đặt bài toán Mạng tế bào với Python
def update_cell(grid, rule, row, col):
"""
Cập nhật giá trị của ô (row, col) trong lưới theo qui luật rule.
"""
if rule == 1:
grid[row][col] = grid[row-1][col] if row > 0 else 0
elif rule == 2:
grid[row][col] = grid[row][col+1] if col < len(grid[0])-1 else 0
elif rule == 3:
grid[row][col] = grid[row+1][col] if row < len(grid)-1 else 0
elif rule == 4:
grid[row][col] = grid[row][col-1] if col > 0 else 0
elif rule == 5:
grid[row][col] = grid[row-1][col] if row > 0 else (grid[row+1][col] if row < len(grid)-1 else 0)
elif rule == 6:
grid[row][col] = grid[row][col-1] if col > 0 else (grid[row][col+1] if col < len(grid[0])-1 else 0)
elif rule == 7:
grid[row][col] = grid[row-1][col] if row > 0 else (grid[row][col-1] if col > 0 else 0)
elif rule == 8:
grid[row][col] = grid[row+1][col] if row < len(grid)-1 else (grid[row][col+1] if col < len(grid[0])-1 else 0)
def update_grid(grid, signal, rules):
"""
Cập nhật lưới theo dãy tín hiệu và qui luật truyền tin.
"""
for i in range(len(grid)):
for j in range(len(grid[0])):
if signal[j] == '1':
update_cell(grid, rules[i][j], i, j)
def main():
# Đọc dữ liệu từ file input
with open('P3.INP', 'r') as f_in:
# Đọc số dòng, số cột, số nhịp thời gian
M, N, T = map(int, f_in.readline().split())
# Đọc dãy tín hiệu vào
signal = f_in.readline().strip()
# Đọc qui luật truyền tin
rules = []
for _ in range(M):
row = list(map(int, f_in.readline().split()))
rules.append(row)
# Khởi tạo lưới với giá trị ban đầu là 0
grid = [[0 for _ in range(N)] for _ in range(M)]
# Cập nhật lưới sau T nhịp thời gian
for _ in range(T):
update_grid(grid, signal, rules)
# Ghi kết quả vào file output
with open('P3.OUT', 'w') as f_out:
for row in grid:
f_out.write(' '.join(map(str, row)) + '\n')
if __name__ == '__main__':
main()
Cài đặt bài toán mạng tế bào với C++
#include <iostream>
#include <fstream>
#include <vector>
#include <string>
using namespace std;
// Hàm kiểm tra xem một ô có nằm trong lưới hay không
bool isValid(int x, int y, int M, int N) {
return (x >= 0 && x < M && y >= 0 && y < N);
}
// Hàm cài đặt qui luật truyền tín hiệu của lưới
int updateCell(int x, int y, vector<vector<int>>& grid, vector<vector<int>>& rules) {
int M = grid.size();
int N = grid[0].size();
int dx[] = {-1, 1, 0, 0, -1, 1, -1, 1};
int dy[] = {0, 0, -1, 1, -1, 1, 1, -1};
int cnt = 0;
for (int i = 0; i < 8; i++) {
int nx = x + dx[i];
int ny = y + dy[i];
if (isValid(nx, ny, M, N) && grid[nx][ny] == 1) {
cnt++;
}
}
return rules[x][y] == 0 ? grid[x][y] : (cnt > 0 ? 1 : 0);
}
int main() {
int M, N, T;
vector<vector<int>> grid;
vector<vector<int>> rules;
string signals;
// Đọc dữ liệu từ file input
ifstream infile("P3.INP");
infile >> M >> N >> T;
infile.ignore();
infile >> signals;
grid.resize(M, vector<int>(N));
rules.resize(M, vector<int>(N));
for (int i = 0; i < M; i++) {
for (int j = 0; j < N; j++) {
infile >> rules[i][j];
}
}
infile.close();
// Cài đặt trạng thái ban đầu của lưới
for (int i = 0; i < M; i++) {
for (int j = 0; j < N; j++) {
grid[i][j] = signals[0] - '0';
}
}
// Cập nhật trạng thái của lưới sau T nhịp thời gian
for (int t = 0; t < T; t++) {
vector<vector<int>> nextGrid = grid;
for (int i = 0; i < M; i++) {
for (int j = 0; j < N; j++) {
nextGrid[i][j] = updateCell(i, j, grid, rules);
}
}
grid = nextGrid;
}
// Ghi kết quả vào file output
ofstream outfile("P3.OUT");
for (int i = 0; i < M; i++) {
for (int j = 0; j < N; j++) {
outfile << grid[i][j];
}
outfile << endl;
}
outfile.close();
return 0;
}

